Some insights
 The Counter-Revolving Twins
Two spaceships, A and B, are in circular orbits, revolving in opposite directions.  Twice each orbit, they pass each other.  The astronauts on ship A peek in the windows of ship B each time they pass and look at the clocks.  And what do they see?  Ship B's clocks are running slow.  Never mind for the moment what ship B's astronauts see when they look in the windows of ship A -- this by itself is quite interesting because, no matter how long the ships stay in orbit, when they pass their clocks are still in sync!  When do the clocks on  ship B catch up with the clocks on ship A?

The question is real, and so is the effect -- it's not just an illusion.  Suppose there's a clock in the nose and the tail of each ship, and suppose that the "nose clocks" are in sync when they pass each other.  Then when the astronaut in the tail of ship A looks at ship B's nose clock, he'll see that it's slow -- it hasn't ticked as often as it should have while the ships were passing.  Yet, the next time that clock passes the nose of ship A, it'll be back in sync.

Somewhere in the orbit, the clocks on ship B must run faster than the clocks on ship A, as viewed from ship A's frame of reference.

What's more, when the ships approach each other, ship A can see that ship B's clocks are already running slow, yet they're in sync when the noses of the ships pass.  Therefore, at some point in the orbit, ship B's clocks must be ahead of ship A's clocks.  When does that happen?

Finally, can the astronauts on ship A ever actually see the clocks on ship B running fast?  And can they ever see the clocks on ship B get ahead of their own clocks?

These questions do not seem to be easy to answer.  My first attempts used curved coordinates, much like the ones used in handling the revolving clock. That got me exactly nowhere.  The problem is that the question I'm asking requires figuring out exactly where the "other" ship is at each moment in the MCRF of the ship, for that is the only way we can properly answer -- or even ask -- the question, "Where is the other ship now, and what time is it on the other ship now?"  It's only in flat space, in a non-accelerated frame, that such a question can be well-posed, and can have an answer.

Finally, as far as the questions I've posed here are concerned, the effect of gravity is uninteresting.  It slows the clocks on the two ships equally, it slows a clock in the center of the circle more than it slows the clocks on either of the two ships, it makes the computations harder, and it adds nothing to the apparent paradox or the interest its solution holds (for me, at least).  So, I have assumed that space is flat, and the two ships are blasting furiously with their engines in order to maintain their circular paths.  Of course, their rockets must point directly outward at all times to keep them going in circles (and that's where the logo for this site comes from -- as I'm sure you've already realized).

This is a rather long page, so here's a table of contents:

Discussion of the Method
Coordinate Conventions
Statement of the Problem and Equations of Motion
The Rotated Coordinate System
Finding Ship B at time τA = 0
Ship B's Clock Rate in A's MCRF
Porthole View: Relative Ship Locations
Porthole View: Relative Clock Rates
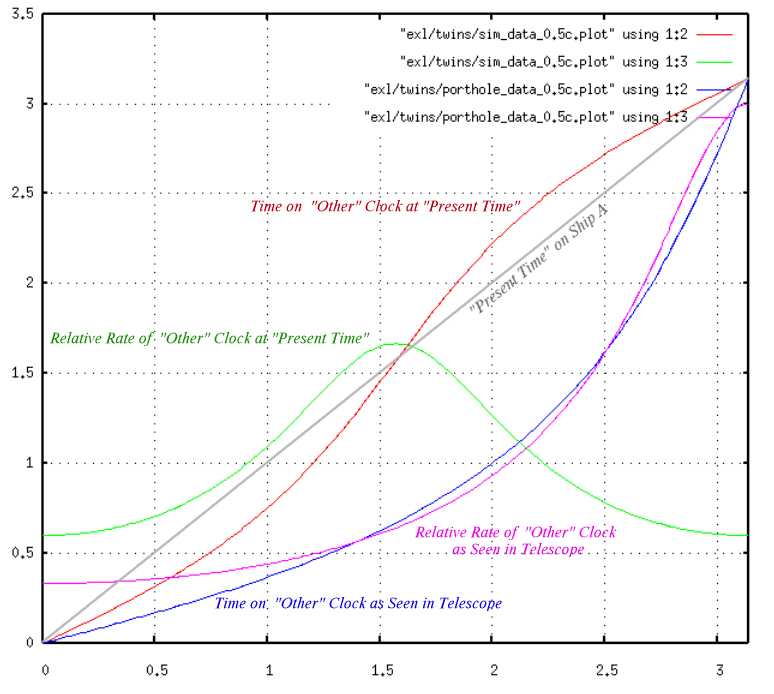
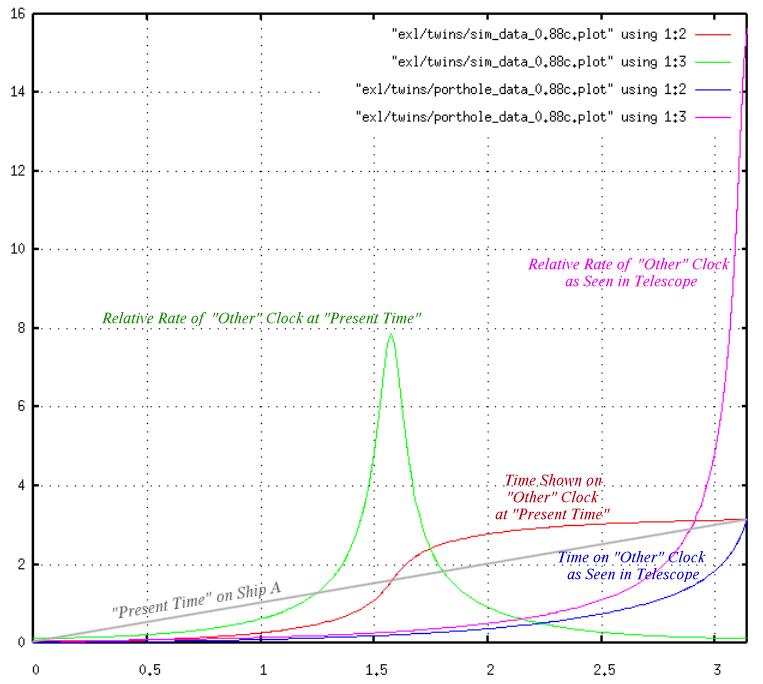
Some Graphs of the Results

Brief Discussion of the Method

There are two ships, A and B, traveling in opposite directions on the same circular path.  There is a single observer in the middle of the circle, referred to as "E" for "Earth" (but we're assuming there's no actual Earth present, and space is flat).

My first goal on this page, and what seems to be the hardest part of the problem, is to determine the location of Ship B in the momentarily comoving reference frame (MCRF) for Ship A at each moment in Ship A's time.  In other words, we need to determine where ship B is "right now" according to Ship A.  Viewed in the Earth frame, the motion of the ships looks like this:

Figure 1:
Diagram 1

To simplify the math, the radius of the circle is assumed to be 1.

Given a particular moment in time in Earth's frame, we will rotate the axes to (ξ, ζ) coordinates, so that ship A lies on the (rotated) ζ axis.  Then Earth time which corresponds to a particular moment in Ship A's MCRF varies with the (rotated) ξ coordinate.  So throughout the Earth frame, we can assign an Earth time which corresponds to the moment we're examining in Ship A's time.  In the Earth frame, we have a simple equation of motion for ship B, so we also can determine the Earth time at which ship B passed each point.  This gives us a system of two equations, and solving it gives us the location of Ship B at A's "present time" in A's MCRF.

This explanation probably does not seem very clear at this point.  Hopefully the meaning will become more apparent as we go through the actual math.

Coordinate Conventions

When we wish to represent a coordinate system which is comoving with Ship A, Ship B, or Earth, we will use a single subscript to indicate what object is stationary in that system.  So,



At a particular moment in time, we're interested in several specific coordinate values.  We need the coordinates of both spaceships in all three frames, and we may need the time coordinate of Earth in all three frames, as well.  We'll use two subscripts to represent each value, where each subscript can be A, B, or E.  The first subscript will indicate what it's a coordinate of; the second will indicate whose frame of reference it's evaluated in.  So we have,



We will adopt the additional convention that the angles θ and φ (see figure 1) are measured only in the Earth frame, so they're not going to be subscripted.

Clearer Statement of the Problem, and Earth-Frame Equations of Motion

We can immediately write the equations of motion for both ships in Earth coordinates, with the assumption that time starts at 0 in all three frames at the moment when the ships simultaneously cross the Y axis:




Equations (4b) and (4c) follow from what we already know of revolving clocks.

Our goal is to find φ as a function of θ.  Exactly what this function should represent is a little hard to describe in words, but I will try.

Consider the MCRF for Ship A at the moment when Ship A is at angle θ.  Suppose this (inertial) frame is populated with observers who fill all space, and that they have all previously synchronized their clocks.  At the moment when Ship A is at angle θ, and is comoving with this frame, exactly one of the observers in this frame will find himself to be standing at the location of Ship B.  That observer -- the one standing next to ship B -- sets off a flare.

In the Earth frame, we observe the flare.

The angle φ which is the location of the flare on the unit circle, as observed from the Earth frame, is the value we are looking for.  It represents the location of Ship B at the moment when ship A is at angle θ, as viewed from ship A.  Note that in general,



To see this, consider that the angular velocity of each ship, viewed in the Earth frame, is exactly proportional to the rate at which that ship's clock is ticking.  But the observers on Ship A saw that Ship B's clock was ticking slowly.  Therefore, at the moment when the ships passed, Ship A's observers saw that Ship B was moving more slowly than Ship A relative to Earth.  That means that if the location of Ship B in A's MCRF were mapped into Earth coordinates,  and we obtained φ for that position, that φ would be found to be growing less rapidly than θ.

To put this yet a different way, the position of Ship B as viewed from Earth, immediately after the ships pass each other, must represent a future position of the ship as viewed from Ship A.  Or, if we were to convert the coordinates of Ship B as viewed from Earth into MCRF coordinates for Ship A, we'd find that the time value did not match the time value of Ship A at that moment in A's own MCRF.  This is really just relativity of simultaneity, but it's taking place on a curve and is therefore harder to picture.

Enough explanation -- let's go on with the derivation.

The Rotated Coordinate System (τ, ξ, ζ)

We introduce rotated and translated coordinates.  We rotate the spacial coordinates by θ and subtract tAE from the time.

Figure 2:
xi and zeta axes


In the inertial frame of Earth, we have



The MCRF for ship A is moving to the left along the ξ axis at velocity v, so the Earth frame is moving to the right relative to ship A's MCRF, and:



Finding Ship B at Time τA = 0

We need to find the locus of all events in the Earth frame which occur simultaneously with ship A passing through angle θ, in the frame of reference of ship A.  In other words, we want to find the Earth coordinates for all points for which τA = 0.  With that restriction, equations (7a) and (7b) reduce to



From figure 2, we can find the ξ coordinate of ship B in Earth's FoR as a function of the angles:



But we also know the location of Ship B in Earth's FoR as a function of its Earth time coordinate:



From equations (8a) and (11),



Substituting (9) into (12),



and substituting for δE, finally we obtain the exact solution as an implicit function,

and, for small values of v,


Later on I'll plug the exact formula (15) into a program to get some graphs of what the ships are doing.  We can see the general form of the behavior by inspecting equation (16), however.

The ships pass when θ = 0 and θ = π, and at both of those points φ = θ, as it must.  The two angles are also equal when θ = π/2, and for values between π/2 and π, ship B is ahead of ship A, as viewed from ship A's MCRF.

Note that at π/2, the two ships are traveling parallel to each other.  The "line of simultaneity" in their MCRFs passes through both ships and the observer in the middle of the circle -- the event of crossing angle π/2 is simultaneous for both ships in all three frames of reference.  So, at that point we would expect to have φ = θ, and in both (15) and (16) we see that is the case.

The Rate of Ship B's Clock, in A's MCRF

Viewed from the Earth frame, the clock rates of A and B are constant, as are their angular velocities.  The angles θ and φ are measured in the Earth frame, and are thus proportional to the elapsed proper times on ship A and ship B.  We can therefore use the angles as proxies for the times, since we are only concerned here with the relative rates between the two ships.

First, from (16) we have immediately the approximate solution,

Differentiating (15) we obtain the exact solution as a function of θ and φ:



and finally,

As we might have guessed from the fact that Ship B falls behind initially, but catches up and passes ship A's angular position at the point when they're opposite each other, ship B's clock runs fastest relative to A's at the moment when they are traveling parallel to each other.  At that point, θ = π/2, cos(2θ) = -1, and equation (17) reaches a maximum.  That's when B is "passing" A, and that's when it's going fastest.  A casual inspection of equation (19) reveals that as v approaches 1, the ratio of the clock speeds at the moment when the ships are directly across from each other approaches infinity.

This is very surprising!  At the moment when B's clock is zooming ahead, the relative velocity between A and B is zero!

Intuitively we might expect the clock rates to match at that point, since the ships are relatively stationary.  However, intuition fails badly in this case, because both ships are accelerating, and when we try to take the consequential rotation of the reference frames into account we see that Ship B is actually moving very quickly across the "line of simultaneity" between it and ship A.  And the consequence is that its time is changing rapidly relative to ship A's time.  (But as always, be cautious with all "intuitive" explanations when dealing with relativity!)

Again, I'll plug formula (19) into a program a little later and get some graphs out.

The Porthole View: Relative Ship Locations

Suppose the astronauts on Ship A point a telescope out the window and watch ship B.  What do they actually see?

This is much simpler than the previous question, since we can do it entirely in the frame of reference of the Earth (central) observer.   All we need to determine is when a pulse of light sent from Ship B will arrive at ship A, or, equivalently, we need to determine at what angle φ the pulse must be emitted by ship B in order to be received at angle θ by ship A.

Figure 3:
Path of the Photon

Ship B sends the pulse at time



and it's observed by Ship A at time



and the total pathlength, by simple trigonometry, must be



Since C=1, the time it takes the photon to traverse the path is P.  Therefore, in the Earth frame, the time when the photon reaches A must be later than the time it left B, by P:



Substituting (20) and (21) into (23b) and combining with (22), we get


and finally

or, for small values of v,

It's obvious from these formulas -- and from simply looking at Figure 3 -- that Ship A can never see a "future" reading on Ship B's clock.  As θ runs from 0 to π/2, sin(θ) is always positive, and hence the observed value of φ is always less than θ.

Note that if this were not true, then due to the symmetry of the situation, information could be sent from ship B to ship A and back, and arrive back at ship B before it left!

This is in stark contrast to the MCRF view, in which Ship B's clock does, indeed, get ahead of Ship A's clock.  But it happens only when the ships are separated spatially, and by the time the image of the clock can get from B to A, A's clock has caught up.  So, again, observers on Ship A can never actually see a later reading on Ship B's clock -- they can just deduce the existence of such a reading by working out what time their clock read when Ship B emitted the light pulse they have just received.

The Porthole View:  Relative Clock Rates

Differentiate (25) to obtain the ratio of the clock rates:



and finally

or for small values of v,

In contrast to the actual clock readings, the observers on A can indeed see Ship B's clock running fast.

This is hardly surprising -- it's just the blue shift of the signals from Ship B when the ships are moving toward each other.

Some Graphs

The exact formulas I derived above are implicit -- they haven't been solved for φ in terms of θ alone.  That makes it a little hard to see what's actually going on.  To get a better feel for it, I plotted the functions for a couple values of v.

The program is a trivial Newton's Method solver,  in three files.  It's hardly a work of art, but if you want to look at it, it's here:
twins.cxx
twin_solve.cxx
twin_solve.h
The plots were done via direct commands issued in Gnuplot.

I plotted data for 0.5C and for 0.88C.  The colored labels on the traces were added with Gimp, which was also used to jpg the plots afterward.  The line representing "present time" on Ship A's clock was also added with Gimp.  No other changes were made.  The weird trace labels in the upper right corner will be familiar to anyone who's used Gnuplot.

Both axes on each graph show radians, viewed from the Earth frame, which act as a proxy for the ship's times.

Graph 1 -- Data for 0.5C:

Plot for 0.5c
As expected, the relative rate of Ship B's clock is at a maximum at the point when the ships are running parallel, and are farthest apart.  The line labeled 'Time on "Other" Clock at "Present Time" is the time seen by an observer in the MCRF of Ship A who happens to be standing next to Ship B, and whose clock shows the same reading as Ship A's clock.  Whenever that curve is above the gray "Present Time" line, Ship B's clock is ahead of ship A's clock:  in other words, B's clock is ahead for the entire second half of the semicircle.  In contrast, the blue "Time on Other Clock as Seen in Telescope" line never crosses the "present time" line -- the observed time is always behind the current time.

The clock rate lines indicate ship B's clock is running faster than ship A's whenever they're higher than 1.  The green "Relative Rate" line, which is the value computed by the observers on ship A, peaks at π/2, as we expected.  The relative rate as seen in a telescope (magenta line) peaks just as the ships meet -- it's the blue shift, and it's most extreme at the moment when the ships are heading directly toward each other.

Finally, note that this is one cycle of a periodic graph.  If we glue another copy onto the right-hand edge, we noticed something a little surprising, which is that the line showing the rate as seen in the telescope is discontinuous!  At the moment when the ships pass each other, the observed rate drops abruptly, as the blue shift changes to red shift.  In practice, unless the ships actually collide there will actually be a smooth transition from blue shift to red shift as they pass "near" each other.


Graph 2 -- Data for 0.88C:
Data plot for 0.88C

This graph shows nothing new, except for the perhaps unexpectedly sharp peak on the computed relative rate curve (green), and the skyrocketing value of the observed rate curve (magenta).